月份: 2021 年 5 月

※廣告預算用在刀口上，台北網頁設計公司幫您達到更多曝光效益

擁有後台管理系統的網站，將擁有強大的資料管理與更新功能，幫助您隨時新增網站的內容並節省網站開發的成本。

劉軍（右一）帶領高蹺隊在襄陽唐城影視城表演。 　　劉 江攝

　　追夢人：劉  軍

　　46歲，湖北省南漳縣東鞏鎮蓮花村村民，13歲隨父學習高蹺，現在每逢年節，便帶領高蹺隊走街表演……

　　得意事一

　　把高蹺玩出了名氣

　　隆冬時節，湖北南漳山中雨雪連綿，氣溫降至零攝氏度以下。劉軍惦記着農曆“小年”的表演，雞叫時分就起了床，綁上高蹺，在院中活動起腿腳來。

　　早在一個月前，劉軍就接到了通知，臘月二十四上午要帶隊去縣城表演。這是劉軍每年春節的“例行安排”——從“小年”開始，他的生活便會被高蹺填滿，從蓮花村到東鞏鎮，再到南漳縣、襄陽市，直到農曆二月二龍抬頭，他才有時間忙自己家裡的事情。

　　農家早飯遲。走了幾圈不過癮，劉軍索性拿起手機吆喝鄧明松、張衛、金艷軍等隊友前來排練。

　　東鞏高蹺與別處不同，文蹺重在說唱有趣，武蹺講究驚險刺激，稍有不慎，傷人不說，還可能砸了招牌。劉軍能文蹺，更擅武蹺，看他表演，驚險處讓人大氣不敢出。比如一人踩蹺從另一人小腹踏過的“仙人過肚”，五人層層疊高拱手作揖的“五子登科”等造型，他和隊友們配合無間，一一完成。

　　“從我跟父親學藝開始就被教導，越是老師傅，越要謹慎小心。”劉軍說，從藝30多年他沒有出過丑，靠的就是熟能生巧和膽大心細。

　　一連十幾場迎春表演，一招一式都馬虎不得。臨近年節，每天不踩上高蹺走幾圈，劉軍心裏就不踏實。

　　劉軍自稱平生最得意事有三，第一個就是踩高蹺。“本來是當作業餘愛好來玩，沒想到玩出了名氣，玩成了副業。”

　　東鞏鎮民間文化氛圍濃厚，有“古山寨之鄉”的美譽，不僅有春秋寨、卧牛寨等龐大的古山寨群，還有麻城河等連片古村落群。近些年，鄉村旅遊興起，高蹺成了深居荊山的古山寨開門迎客的特色節目，劉軍的高蹺隊常常接到表演邀請，一場一人100元。

　　劉軍一家，個個能踩高蹺。他自己是東鞏高蹺的市級非遺傳承人，正在湖北文理學院讀聲樂本科的兒子劉朝旭則是縣級傳承人，兩個人每年還能拿到南漳縣文化局發放的2500元補貼。

　　“趕上新時代，老藝術有了新生機。”劉軍說，以前老擔心自己的高蹺絕活失傳，沒想到“現在踩高蹺能當飯吃了，學的人越來越多”。如今，劉軍剛滿10歲的侄子和外甥放了假就會跟着他學踩高蹺。

　　得意事二

　　山裡路好了，貨車有了用場

　　南漳縣曾是省級貧困縣，“八山半水分半田”，农民生活不易。“打我記事起，家裡就為吃口飽飯發愁。”劉軍說，他父親踩高蹺一為興趣，二為生活，走街串戶討彩頭，人家會給點煙酒或食物做報酬。

※廣告預算用在刀口上，台北網頁設計公司幫您達到更多曝光效益

擁有後台管理系統的網站，將擁有強大的資料管理與更新功能，幫助您隨時新增網站的內容並節省網站開發的成本。

　　如今，劉軍踩高蹺只為興趣，表演所得只是其家庭收入的一小部分。

　　吃過早飯，劉軍發動停在家門口的貨車，出工了。鄰村有一戶蓋房子，訂了他的車運建材，這一單能掙小几千元。

　　6年前買這輛二手的中型貨車，是劉軍最得意事中的第二項。當時，南漳的大山裡，易地扶貧搬遷如火如荼，劉軍奔波在多個工地上搞運輸，6.8萬元的買車錢一年就回了本。

　　劉軍感嘆，若不是“四好農村路”通到了家家戶戶的門口，他的這輛車就“抓瞎了”。在2014年以前，東鞏鎮的村寨還是以泥巴路為主，遇到雨雪天氣，“別說載重十幾噸的大貨車，就是自行車都難推動”。

　　路好，山裡的生活就越來越好。

　　農村人把房子當做臉面，外出打工掙了錢，都想着回村到公路邊蓋新房子。正因如此，劉軍趕上了好年景，四鄰八村建新房，都找他運建材，一年有個八九單，就能掙三四萬元。

　　得意事三

　　釀“武蹺神”酒

　　出一趟車回來，劉軍顧不得吃午飯，先去了自己家的小酒廠。因為天氣太冷，釀酒的鍋爐已停，煮好的糧食堆在池子里發酵。

　　釀酒，是劉軍第三件得意事。他用當地世代相傳的古法釀酒技術，經過現代技藝改良后，酒香更濃，口感更潤。

　　說是酒廠，實際上是個作坊，3間房，一年產量有15000多斤。“根本不愁賣，每到這個時候就供不應求。”劉軍說。苞谷酒順着他的貨車和高蹺表演香飄四鄉，已經打開了市場。

　　他把這酒命名為“武蹺神”。“釀酒跟踩高蹺一樣，不能貪心，不能偷工減料，否則就會傷人傷己。”劉軍說，踩高蹺的道具只是兩根50—90厘米長、上扁下圓的木棍，看似簡單，但對選材要求很高，必須採用堅硬而有韌性的木質，腐木絕不可用。

　　靠賣酒，劉軍一年可掙5萬多元。隨着銷量越來越好，原有的作坊已經不能滿足供應，劉軍在周邊買了2畝地，準備新的一年擴大規模。在釀酒作坊的院子里，劉軍新買的40口酒缸在陽光下閃着光。那是酒廠擴大規模后，用來洞藏的酒具。

　　新的一年，劉軍希望帶領蓮花村高蹺隊讓東鞏高蹺的名聲傳向全國，也希望帶着自己的“武蹺神”在鄉村振興中干出更大的成績。

　　劉軍的記事本

　　趕上新時代，老藝術有了新生機，現在踩高蹺都能當飯吃了。

　　過去，父親踩高蹺是為生活；如今，我踩高蹺，卻是為興趣。

　　版式設計：張丹峰  蔡華偉

本站聲明:網站內容來http://www.societynews.cn/html/wh/fq/,如有侵權,請聯繫我們,我們將及時處理

※廣告預算用在刀口上，台北網頁設計公司幫您達到更多曝光效益

擁有後台管理系統的網站，將擁有強大的資料管理與更新功能，幫助您隨時新增網站的內容並節省網站開發的成本。

※廣告預算用在刀口上，台北網頁設計公司幫您達到更多曝光效益

有別於一般網頁架設公司，除了模組化的架站軟體，我們的營業主軸還包含：資料庫程式開發、網站建置、網頁設計、電子商務專案開發、系統整合、APP設計建置、專業網路行銷。

　　今天是2020年2月12日星期三，現在對學習有點麻木。看了一天的最大熵模型，多少理解了一些內容，在學校看的啥啊真是，要不是寫這個博客，關鍵的地方真是一點看不出來啊。反思再反思，看書的時候難懂的地方直接翻過去了，現在為了寫出來，多查了很多資料。切忌眼高手低啊，不把模型真正用出來，很難有深入的理解啊。

　　本章標題為邏輯斯諦回歸與最大熵模型，這是兩個部分，不能混為一談。當然了放在一起肯定有李航老師的道理，最後會分析兩者聯繫。最大熵模型還是比較難懂的，這裏僅是記錄我的學習過程，歡迎討論，僅作參考，謝絕採納。

 GitHub：https://github.com/wangzycloud/statistical-learning-method

 邏輯斯諦回歸模型

引入

　　首先要說下，“邏輯斯諦”這個名字真是蠻奇怪的，可能因為我還是比較沒文化吧。腦子里先入為主，總是想把吳恩達老師CS229上邏輯回歸算法的名字安放到這個模型上。所以接下來，都會以“邏輯回歸”這個名字代替書中的“邏輯斯諦回歸”。不得不說，該算法從一個特殊的函數出發，發現了可將輸入變量x的線性函數值轉變為分類類別的概率。

邏輯斯諦分佈

　　首先來看一下這個邏輯斯諦分佈和概率密度函數：

　　分佈函數屬於邏輯斯諦函數，圖形像一條S型曲線，在中心附近增長較快，在兩端增長速度較慢。形狀參數γ的值越小，中心附近增長越快。 

二項邏輯回歸模型

　　作為分類模型，顧名思義，二項邏輯回歸模型是一種二分類算法，由條件概率分佈P(Y|X)表示，隨機變量X取實數，隨機變量Y取值為0或1。

　　這裏得出類別結果的過程與樸素貝恭弘=叶 恭弘斯算法類似（這裏強調的是，需要得到P(Y=1)和P(Y=0)，兩算法本身差別很大），每個類別都要求出該類的條件概率，然後比較大小得到分類結果。對於給定的輸入實例x，分別求得P(Y=1|x)和P(Y=0|x)，比較兩個條件概率值的大小，將實例x劃分到概率值較大的類中。而感知機、決策樹是直接得到類別。

　　接下來，從事件發生幾率的角度上，看一下邏輯斯諦函數的特殊性。

　　一個事件發生的幾率是指該事件發生的概率與不發生的概率的比值，如果事件發生的概率是p，那麼該事件的幾率是p/(1-p)，其對數幾率或logit函數是：

　　有了對數幾率的函數表達形式，我們將二項邏輯回歸模型的表達式代入，得到：

　　可以發現，輸入實例x與該實例被判斷成Y=1這個類別的對數幾率，竟然是線性關係。換句話說，輸出Y=1的對數幾率是由輸入x的線性函數決定的，這就是邏輯回歸模型的來源。正如書中所描述的，換一個角度看，考慮對輸入x進行分類的線性函數w·x，其值域為實數域。擬合參數w，使輸入數據x可以找到一個決策邊界，這個邊界是由對數幾率表現出來的。直觀來說，屬於正類的數據，通過w的線性變換，得到一個很大的實數值，因此該數據表現為判斷是正類的對數幾率大。通過公式6.5，可以將w·x的線性函數值轉換為概率：

　　這時候，線性函數w·x的值越接近正無窮，概率值越接近1；w·x的值越接近負無窮，概率值越接近0，這樣的模型就是邏輯回歸模型。

模型參數估計

　　根據以上描述，我們擁有了新的分類模型，可以將w·x的線性函數值轉化為類別的概率，那麼，我們如何找到分類邊界呢？也就是說，我們現在擁有了輸入x到類別概率的映射模型，可是怎麼保證每個隱射關係都是對的呢？通俗點講，每一個輸入實例x，乘參數向量w之後的線性函數值，轉化為類別後都能夠被正確分類。關鍵的問題，也就是在w，如何對w進行估計？這裏採用極大似然估計。

　　似然函數很好理解，進行極大似然估計，需要把每個變量出現的概率連乘起來；連乘式里的表達式，中括號分開的兩個部分，在同一個實例上，不會同時成立；式一，實例類別yi=1時，左側中括號內概率成立，右側值為1；實例類別yi=0時，右側中括號內概率成立，左側值為1。通過這一個式子，就把兩個類別出現的概率連乘在了一起。

　　這樣，尋找合適w的過程（尋找決策邊界）就變成了以對數似然函數為目標的最優化問題，常用的方法是梯度下降法和擬牛頓法。

多項邏輯斯諦回歸

　　涉及到多分類的邏輯回歸模型，該部分有待深入思考公式，留到開學后。

最大熵模型

引入

　　我更喜歡把這部分內容當做原理，說這個模型的具體應用吧，我這個水平還沒有發現。但了解過大概思想后，發現這個模型應該在概率模型中處處存在。最大熵最大熵，顧名思義要讓熵最大，延續先前的知識，熵是不確定性的度量，最大熵模型也就是要找出熵最大某個物件。學習之前先提出疑問，比如一個簡單的問題，從哪裡找到熵最大？熵最大的什麼？我剛開始看到這個模型的時候，習慣性的向後翻了翻課本，上來就被數學公式嚇到了（靜下心來發現沒必要這樣），仔細閱讀一遍之後，除了“什麼都沒看懂”之外，什麼都沒懂。

　　所以在開始記錄之前，有必要先強調一下，該模型從原理出發，討論的是一個概率模型的學習準則問題。假設現在我們有一個分類問題（必須是概率模型），比如說邏輯回歸進行分類，我們最後通過比較類別的可能性大小，對新實例做出判斷。我們的學習過程，是找到合適的w，從而讓所有的數據點，能夠得到完美的分類。在邏輯回歸模型中，我們是通過極大似然估計，來找到合適的w，而現在我們的最大熵模型，反映的是什麼呢？

　　有了剛才的例子，其實我們可以發現，訓練集上每一個w代表了一個模型，只不過呢，有的w分類能力很好（最好的被我們用極大似然估計選擇了出來）；有的呢，分類能力很差，不被我們採納。本節提到的最大熵模型，就是從滿足條件的模型集合中選出熵最大的模型，我們認為這個熵最大的模型就是最好的模型。簡單點，就是從一堆w中，運用熵最大原理找出這個最合適，分類能力最強的w。

最大熵原理

　　最大熵原理認為，學習概率模型時，在所有可能的概率模型中，熵最大的模型是最好的模型，通常用約束條件來確定概率模型的集合。所以，最大熵原理也可以描述成在滿足約束條件的模型集合中選取熵最大的模型，該原理是概率模型學習的一個準則。

　　解讀一下這段。首先，我們針對的是類似邏輯回歸、樸素貝恭弘=叶 恭弘斯這樣的概率模型，不是針對感知機這種決策函數模型。其次，熵最大也就是不確定性最大，這好像與我們的目標相悖，畢竟我們是要找到一個明確的分類邊界，現在怎麼又要找不確定性最大的呢？這裏也挺好理解的，我們在什麼情況都不知道的處境下，當然不能偏袒任何一個類別，雨露均沾才能損失最小。如果太過於相信其中一個，萬一是假的不就一敗塗地了嘛，一點後退的餘地都沒有。不偏袒任何一個類別就意味着誰都不信，每個的可能性一樣，這個時候熵最大，這是公知的。另外，在每個類別可能性一樣的前提下得到的模型，對給定實例x進行判斷，這時某類的概率還能較大，不更能說明x應該屬於這類。最後，我們在訓練數據集中學習一個模型，怎麼可能一點前提條件都不知道！多多少少有一些特徵是我們先知道的，或者說是作為已知條件的。我們要學習的模型，就是在已知的這些條件下，找到最合適的分類模型（應用熵最大原理）。

　　直觀的，最大熵原理認為要選擇的概率模型首先必須滿足已有的事實，即約束條件。在沒有更多信息的情況下，那些不確定的部分都是“等可能的”，最大熵原理通過熵的最大化來表示可能性。書中提到，“等可能”不容易操作，而熵則是一個可以優化的數值指標，這裡有待思考（好像事實就是這樣）。看一下例子：

　　書中又用了一個幾何例子解釋，正是這個幾何例子，放大了對初學者的不友好。看一下書中的解釋：

　　一個點代表一個模型，請問，點在哪裡？整個單純形代表模型集合，請問，是用面積還是邊長？直線的交集對應於滿足所有約束條件的模型集合，請問，直線與直線相交，難道不是個點嗎？最後一句，學習的目的是在可能的模型集合中選擇最優模型，最大熵模型則給出最優模型選擇的一個準則，拜託，這句話說了多少遍了，和這個幾何解釋有什麼關係？不友好就是不友好，雲里霧裡的（也可能是我沒文化，看不懂數學語言）。可是，如果換一種說法，如下圖：

　　不妨讓區域p表示概率模型空間，也就是所有的模型圈在這個三角形區域中（左側）；有一個約束條件，我們就畫一條線（右側藍綠色直線）；約束條件會把模型限制在不同區域（A、B、C、D），約束條件越多，符合條件的模型越少；假設A區域符合約束條件，之前需要從大範圍的p區域求最優模型，現在需要在小範圍的A區域求解。

最大熵模型的定義

　　最大熵原理是統計學習的一般原理，應用到分類問題，得到最大熵模型。給出定義前，我們先來思考一下，按照前邊描述的思想該模型應該有什麼？(1)該模型解決分類問題，要應用在概率模型上，那麼我們的目標就應該類似樸素貝恭弘=叶 恭弘斯算法，用條件概率分佈P(Y|X)表示分類模型。(2)原理部分一直提約束條件，細想一下約束條件可以幫助我們縮小求解範圍，的確符合現實意義，可是要怎麼找到約束條件呢？留疑。(3)要在所有模型中找到熵最大的模型，用什麼熵？衡量模型？(4)如何計算？

※Google地圖已可更新顯示潭子電動車充電站設置地點!!

日本、大陸，發現這些先進的國家已經早就讓電動車優先上路，而且先進國家空氣品質相當好，電動車節能減碳可以減少空污

　　帶着問題，我們系統性的看一下最大熵模型的定義。首先是分類模型的定義：

　　分類模型就是我們最後對新數據進行測試的模型，應該是P(Y|X)這個樣子。對於一個二分類的新測試實例x，若第一類的條件概率P(y1|x)=0.7，第二類的條件概率P(y2|x)=0.2，有0.7>0.2，我們認為實例x屬於第一類。接下來我們尋找約束條件，下述內容（除課本內容外）為個人見解，正確性不能保證。

　　大膽假設，小心求證，這裏我們借鑒一下樸素貝恭弘=叶 恭弘斯的東西，來提出約束條件。我們要做的事情，是找到熵最大的分類模型，分類模型是P(Y|X)條件概率分佈；樸素貝恭弘=叶 恭弘斯是種生成模型，它應用X、Y的聯合概率找到生成數據的方式，求解P(Y|X)來計算類別的后驗概率；數據集上存在X、Y的聯合分佈（經驗分佈）；數據集上存在X的分佈（經驗分佈）；這裏隱約存在一種關係：P(A,B)=P(Y|X)P(X)；在數據集固定的情況下，我們已知P(X,Y)、P(X)經驗分佈，要求的熵最大的條件概率P(Y|X)是不是要滿足聯合分佈規律呢？

　　答案是一定的，P(A,B)=P(Y|X)P(X)規定了一定存在一個條件概率P(Y|X)分佈，使該式成立。現在我們不知道它具體是什麼，需要我們求解出來，在求解的過程中，我們猜測的所有條件概率分佈，都要滿足這個約束才對。

　　約束條件好像是找到了，現在還差個東西。記得我們在素樸貝恭弘=叶 恭弘斯算法中，求過隨機變量X和隨機變量Y同時出現的聯合分佈，那時通過極大似然估計對參數求解，事件X和事件Y同時出現這件事，直接計算聯合分佈了。我們現在的最大熵模型，比較理論化，需要抽象出一個描述聯合分佈的工具，這個工具不幹別的，就是描述數據集中的x、y是否同時存在，是否滿足某一事實，是否具有該特徵。看一下書中內容：

　　便於數學形式表達，設計特徵函數來表達隨機變量X與隨機變量Y的取值，同時發生的事實。（這裏插一句，在CRF條件隨機場中，有個定義在最大團上的勢函數，完全可以用來理解這裏的特徵函數；另外，CRF中的勢函數更可以用這裏的特徵函數來理解；LR和CRF的區別值得好好研究，LR中的W是對特徵向量的各個分量進行線性變換，CRF中的W是對定義在最大團上的關聯進行線性變換…嘚啵嘚…嘚啵嘚…）

　　在剛才P(A,B)=P(Y|X)P(X)的描述中，是拿聯合分佈當做引子，來理解從哪裡來的約束條件。在實際的模型，並不是硬性從分佈函數相同入手，而是落到具體的數值上（具體的特徵上），讓期望相等作為模型的約束條件（分佈相同，期望相同）。

　　這裡是數據集上聯合分佈的期望值。

　　這是數據集上的隨機變量X的邊緣分佈與分類模型P(Y|X)乘積的期望值。

　　如果分類模型P(Y|X)能夠應用到該數據集上，就可以假設P(A,B)=P(Y|X)P(X)公式兩邊的分佈，對特徵函數f(x,y)的期望值相等。這樣，就可以將公式6.10或公式6.11作為模型學習的約束條件，假設有n個特徵函數，相應的就有n個約束條件。

　　帶有約束條件的模型集合我們能夠確定了，接下來就是對模型P(Y|X)用什麼來度量不確定性，很明顯的，用條件熵就可以了。最大熵模型具體定義如下：

　　該部分還差一點，書中開始部分聯合分佈P(X,Y)的經驗分佈和邊緣分佈P(X)的經驗分佈如何求？了解樸素貝恭弘=叶 恭弘斯算法的同學應該知道，根據大數定律，當訓練集包含足夠多的樣本時，P(X)及P(X,Y)可以通過各事件出現的頻率來估計，其中：

最大熵模型的學習

　　最大熵模型的學習過程就是求解最大熵模型的過程，由公式6.12和公式6.13，求解過程可以形式化為約束最優化問題，即：

　　按照最優化問題的求解習慣，將求最大值問題改寫為等價的求最小值問題：

　　這裏參照書上內容，將約束最優化的原始問題轉換為無約束的對偶問題，通過求解對偶問題求解原始問題。

　　必要的求解過程好像手寫一下，標註出關鍵步驟好像更容易理解，這方面工作開學後會做細緻。暫時直接粘貼過來了，仔細看的話，除了對偶問題的轉化，其它的計算細節就是微積分了，相信是可以看懂的。

　　計算過程沒什麼好解釋的，抄一遍實在沒什麼意思，開學後手寫推導一遍，詳細寫寫計算過程。下面看下例子：

極大似然估計

　　通過原始問題、對偶問題的轉換，我們得到了最優的分類模型：由公式6.22、公式6.23表示的條件概率分佈。下面內容證明一個等價命題：對偶函數的極大化等價於最大熵模型的極大似然估計。證明過程如下：

　　一般似然函數是數據集中各個樣本的聯合概率，本公式給出了似然函數的另一種形式，這個形式需要經過幾個步驟的推導，資料已找到，開學整理上手寫版本，現在只需要知道該對數似然函數是合理的，將求解的最優分類模型帶入似然函數得到：

　　再看一下對偶函數f(w)化簡的結果：

　　可以發現對偶函數等價於對數似然函數，於是證明了最大熵模型學習中的對偶函數極大化等價於最大熵模型的極大似然估計這一事實。

　　到這裏，我們可以得到最大熵模型的一般形式。

　　查資料的時候，經常看到“最大熵模型與邏輯回歸的區別”這個問題，第一遍學完本章內容，腦子里反覆思考這兩個模型的推導過程，深的淺的有了一些想法，目前尚未形成條理的思路，以後有了，再補上吧。書中說最大熵模型與邏輯回歸模型有類似的形式，它們又被稱為對數線性模型，這句話是真的沒看明白，說邏輯回歸是對數線性模型還能理解；可最大熵模型的一般形式，只看到了指數啊，難道是因為求解過程的log，這裏存有疑問。

代碼效果

本站聲明:網站內容來源於博客園,如有侵權,請聯繫我們,我們將及時處理

※超省錢租車方案

商務出差、學生出遊、旅遊渡假、臨時用車!GO 神州租賃有限公司!合法經營、合法連鎖、合法租賃小客車!

※自行創業缺乏曝光? 網頁設計幫您第一時間規劃公司的形象門面

網動廣告出品的網頁設計，採用精簡與質感的CSS語法，提升企業的專業形象與簡約舒適的瀏覽體驗，讓瀏覽者第一眼就愛上她。

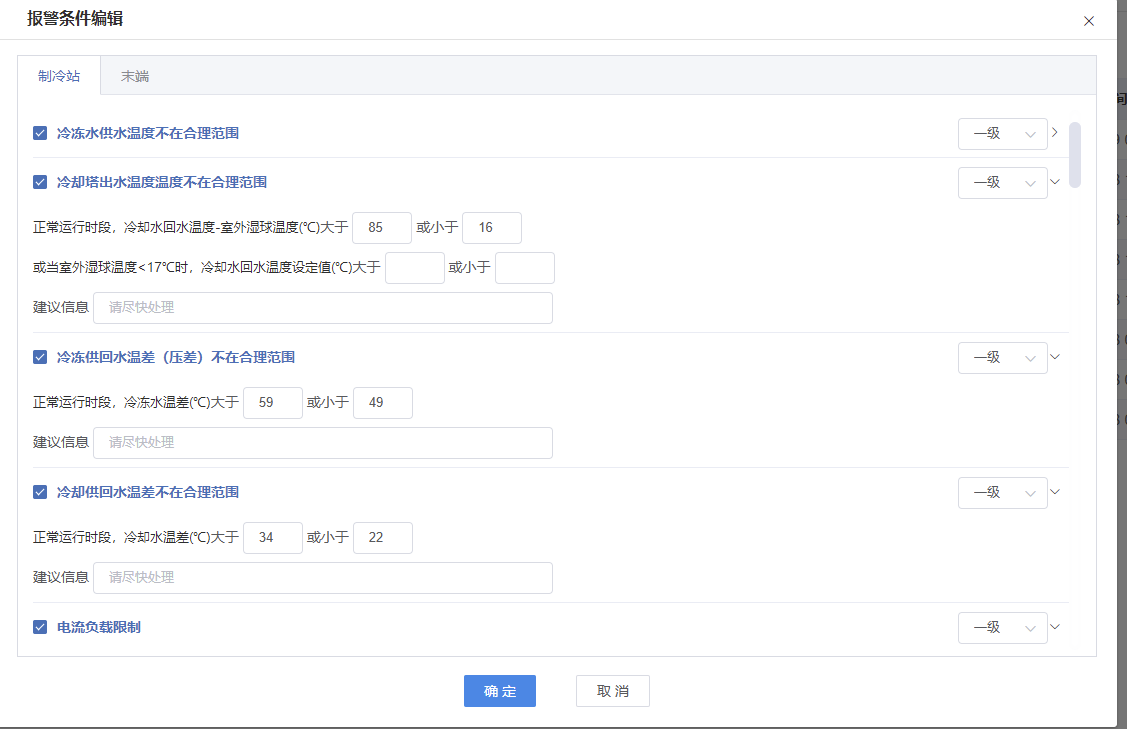
　　需求：點擊一個按鈕，彈出一個模態框，這個模態框有兩個tab，tab中是各種報警條件，這些報警條件是從數據庫中動態取出的，數據庫中數據變更后，這個界面也要變更，我們可以查看和編輯這些報警條件。底部“確定”按鈕點擊的時候，會同時將這兩個tab中的內容都保存到數據庫中去，數據錄入要驗證輸入的格式。

　　對於熟練的人來說，實現其實很簡單，但是對於沒有經驗的人來說，如果按照官網給的那些簡單實例來做，你會發現，出現一些奇怪的問題，諸如，文本框不能編輯內容，表單驗證無效等。感覺elementUI官網的示例太過於粗淺，無法適應實際工作中的許多需求場景。

　　界面效果如下圖所示：

　　分析：用到的組件：el-dialog、el-tabs

 　　AlarmSet.vue代碼：

※產品缺大量曝光嗎?你需要的是一流包裝設計!

窩窩觸角包含自媒體、自有平台及其他國家營銷業務等，多角化經營並具有國際觀的永續理念。

<template>
  <div>
    <div class="alarm-set" v-loading="winLoading">
      <el-tabs v-model="activeName" type="border-card" v-if="alarmTmplData.length>0">
        <el-tab-pane label="製冷站" name="coldSet">
          <ColdSet
            ref="coldSet"
            :alarmTmplData="alarmTmplData"
            @onSubmit="coldSetSummit"
            :showAlarmSetWin.sync="showAlarmSetWin"
          ></ColdSet>
        </el-tab-pane>
        <el-tab-pane label="末端" name="endSet">
          <EndSet
            ref="endSet"
            :alarmTmplData="alarmTmplData"
            @onSubmit="endSetSummit"
            :showAlarmSetWin.sync="showAlarmSetWin"
          ></EndSet>
        </el-tab-pane>
      </el-tabs>
    </div>
    <div slot="footer" class="dialog-footer">
      <div style="display: inline-block">
        <el-button type="primary" @click="onSubmit" :loading="btnLoading">確 定</el-button>
        <el-button @click="isHide">取 消</el-button>
      </div>
    </div>
  </div>
</template>

<script>
import ColdSet from "./ColdSet";
import EndSet from "./EndSet";
import mixinsOption from "@/mixins/mixin-options";
import { alarmService } from "@/services/cold-station-service";
// import { alarmConditionData } from "@/mock/json.js";
export default {
  mixins: [mixinsOption],
  props: {
    showAlarmSetWin: {
      type: Boolean,
      default: false
    },
    alarmTmpl: {
      type: Object,
      default: {}
    }
  },
  components: {
    ColdSet,
    EndSet
  },
  data() {
    return {
      alarmConditionData: [], //報警條件數據
      activeName: "coldSet",
      alarmTmplData: [],
      coldConditionData: [], //冷站報警條件數據
      endConditionData: [], //末端報警條件數據
      isColdValid: false,
      isEndValid: false,
      btnLoading: false
    };
  },
  watch: {
    showAlarmSetWin: {
      handler(val) {
        console.log("showAlarmSetWin", val);
        if (val) {
          this.initData();
        }
      },
      immediate: true
    }
  },
  methods: {
    //初始化數據
    initData() {
      this.$store.commit("base/setWinLoading", true);
      console.log("initData");
      alarmService
        .getConditionList({
          groupNumber: this.groupNumber,
          projectNumber: this.projectNumber
        })
        .then(res => {
          if (res.code === 200) {
            this.alarmConditionData = res.data;
            this.createAlarmTmplData(res.data);
          }
          this.$store.commit("base/setWinLoading", false);
        });
    },
    //構造報警模板數據
    createAlarmTmplData(conditionData) {
      let res = [];
      this.alarmTmplData = this.alarmTmpl.data;
      if (this.alarmTmpl) {
        this.alarmTmplData.forEach(n => {
          // debugger;
          n.descr = eval(n.descr);
          let item = conditionData.find(m => m.tempId == n.id);
          if (item) {
            n["alarmLevel"] = item.alarmLevel;
            n["suggestion"] = item.suggestion;
            n["firstVal"] = item.firstVal;
            n["secondVal"] = item.secondVal;
            n["fourthVal"] = item.fourthVal;
            n["thirdVal"] = item.thirdVal;
            n["status"] = item.status;
          }
        });
      }
      // console.log("this.alarmTmplData :>> ", this.alarmTmplData);
    },
    //確定操作
    onSubmit() {
      this.$refs["coldSet"].onSubmit();
      this.$refs["endSet"].onSubmit();
      if (this.isColdValid && this.isEndValid) {
        this.btnLoading = true;
        let list = this.coldConditionData
          .concat(this.endConditionData)
          .map(m => {
            return {
              tempId: m.id,
              alarmLevel: m.alarmLevel,
              firstVal: m.firstVal,
              secondVal: m.secondVal,
              thirdVal: m.thirdVal,
              fourthVal: m.fourthVal,
              status: m.status,
              suggestion: m.suggestion
            };
          });

        alarmService
          .batchEdit({
            projectNumber: this.projectNumber,
            groupNumber: this.groupNumber,
            list: list
          })
          .then(res => {
            if (res.code === 200) {
              this.$message({
                message: "操作成功！",
                type: "success",
                duration: this.$baseConfig.messageDuration
              });
            }
            this.btnLoading = false;
          })
          .catch(() => {
            this.btnLoading = false;
          });
      }
    },
    coldSetSummit(val, isValid) {
      if (isValid) {
        this.isColdValid = isValid;
        this.coldConditionData = val;
      }
    },
    endSetSummit(val, isValid) {
      if (isValid) {
        this.isEndValid = isValid;
        this.endConditionData = val;
      }
    },
    //取消
    isHide() {
      this.$emit("update:showAlarmSetWin", false);
    }
  }
};
</script>

<style lang="scss" scoped>
.alarm-set {
  height: 600px;
  /deep/ .el-tabs--border-card {
    height: 100%;
  }
  /deep/ .el-tabs__content {
    height: calc(100% - 60px);
  }
}
</style>

重寫elementUI組件樣式，可以使用/deep/ 進行樣式穿透覆寫。

關於表單驗證：由於是動態生成的表單，所以不能按照官網提供的示例來做。

 el-form中不指定驗證規則，而是在el-form-item中指定，如下：
 :prop="`list.${rowIndex}.${fieldArr[2*index+index+1]}`" :rules="rules.numberRule"
 表單數據ruleForm中要對數據進行初始化，否則會無法自動識別數據變化，建議採用深拷貝的形式
考慮到冷站和末端這兩個組件中的代碼可以復用，抽取公共js文件set-mixin.js，然後通過mixins引入，這個類似於組合，還有一種繼承是通過extends來實現。
分析界面雖然是動態的，但是總共只有幾種類型，分別是：1個文本框，2個文本框，沒有文本框。他們都帶有建議信息這一行，所以可以用幾個v-if來區分。

import { alarmLevelOptions, fieldArr } from '@/enum/alarm-enum.js';
import Regexps from '@/utils/regexp.js';
import mixinsOption from '@/mixins/mixin-options';
export default {
  props: {
    alarmTmplData: {
      type: Array,
      default: () => {
        return [];
      },
    },
    showAlarmSetWin: {
      type: Boolean,
      default: false,
    },
  },
  mixins: [mixinsOption],
  data() {
    return {
      levelOptions: alarmLevelOptions(),
      ruleForm: {
        list: [],
      },
      rules: {
        numberRule: [
          {
            pattern: Regexps.commonNumber,
            message: '僅支持3位數和帶1位小數',
            trigger: 'blur',
          },
        ],
        suggestion: [
          { max: 10, message: '長度不能超過10個字符', trigger: 'blur' },
        ],
      },
      fieldArr,
      tmplData: [],
    };
  },
  computed: {
    activeNames() {
      let activeNames = this.tmplData
        .filter((f) => f.descParamType != 0)
        .map((n) => {
          return n.id;
        });
      console.log('activeNames :>> ', activeNames);
      return activeNames;
    },
  },
  methods: {
    initData(type) {
      console.log('initData', type);
      if (this.alarmTmplData.length > 0) {
        this.tmplData = this.alarmTmplData.filter((n) => n.sys == type);
        this.ruleForm.list = JSON.parse(JSON.stringify(this.tmplData));
        // console.log('條件設置initData :>> ', this.ruleForm.list);
      }
    },
  },
};

ColdSet.vue代碼：

<template>
  <div>
    <el-form :model="ruleForm" ref="ruleForm">
      <el-collapse v-model="activeNames">
        <el-collapse-item :name="item.id" v-for="(item,rowIndex) in ruleForm.list" :key="item.id">
          <template slot="title">
            <div class="header">
              <el-checkbox v-model="item.status" :true-label="0" :false-label="1">{{item.name}}</el-checkbox>
              <el-select v-model="item.alarmLevel" size="small">
                <el-option
                  v-for="item in levelOptions"
                  :key="item.value"
                  :label="item.label"
                  :value="item.value"
                ></el-option>
              </el-select>
            </div>
          </template>
          <div class="content vertical">
            <div class="row one" v-if="item.descParamType==1">
              <div class="item" v-for="(subItem,index) in item.descr" :key="index">
                <label>{{subItem}}</label>
                <el-form-item
                  label="大於"
                  :prop="`list.${rowIndex}.${fieldArr[index]}`"
                  :rules="rules.numberRule"
                >
                  <el-input v-model="item[`${fieldArr[index]}`]" size="small"></el-input>
                </el-form-item>
              </div>
            </div>
            <template v-if="item.descParamType==2">
              <div class="row two" v-for="(subItem,index) in item.descr" :key="index">
                <div class="item">
                  <label>{{subItem}}</label>
                  <el-form-item
                    label="大於"
                    :prop="`list.${rowIndex}.${fieldArr[2*index+index]}`"
                    :rules="rules.numberRule"
                  >
                    <el-input
                      v-model="item[`${fieldArr[2*index+index]}`]"
                      size="small"
                    ></el-input>
                  </el-form-item>
                  <el-form-item
                    label="或小於"
                    :prop="`list.${rowIndex}.${fieldArr[2*index+index+1]}`"
                    :rules="rules.numberRule"
                  >
                    <el-input
                      v-model="item[`${fieldArr[2*index+index+1]}`]"
                      size="small"
                    ></el-input>
                  </el-form-item>
                </div>
              </div>
            </template>

            <div class="row one">
              <el-form-item
                label="建議信息"
                :prop="`list.${rowIndex}.suggestion`"
                :rules="rules.suggestion"
              >
                <el-input
                  v-model="item.suggestion"
                  class="max-width"
                  size="small"
                  placeholder="請儘快處理"
                ></el-input>
              </el-form-item>
            </div>
          </div>
        </el-collapse-item>
      </el-collapse>
    </el-form>
  </div>
</template>

<script>
import { alarmLevelOptions, fieldArr } from "@/enum/alarm-enum.js";
import Regexps from "@/utils/regexp.js";
import { validateVal } from "@/utils/validate-utils.js";
import { alarmService } from "@/services/cold-station-service";
import setMixin from "./set-mixin";
export default {
  mixins: [setMixin],
  watch: {
    alarmTmplData: {
      handler(val) {
        console.log("showAlarmSetWin cold :>> ", val);
        if (val) {
          this.initData(1);
        }

         else{            this.$refs[“ruleForm”].resetFields();         }

      },
      deep:true,
      immediate: true
    }
  },
  methods: {
    onSubmit() {
      console.log("冷站確定 :>> ");
      this.$refs["ruleForm"].validate(valid => {
        if (valid) {
          console.log("驗證成功");
          this.$emit("onSubmit", this.ruleForm.list, true);
        }
      });
    }
  }
};
</script>

<style lang="scss" scoped>
@import "./set.scss";
</style>

EndSet.vue：

<template>
  <div>
    <el-form :model="ruleForm" ref="ruleForm">
      <el-collapse v-model="activeNames">
        <el-collapse-item :name="item.id" v-for="(item,rowIndex) in ruleForm.list" :key="item.id">
          <template slot="title">
            <div class="header">
              <el-checkbox v-model="item.status" :true-label="0" :false-label="1">{{item.name}}</el-checkbox>
              <el-select v-model="item.alarmLevel" size="small">
                <el-option
                  v-for="item in levelOptions"
                  :key="item.value"
                  :label="item.label"
                  :value="item.value"
                ></el-option>
              </el-select>
            </div>
          </template>
          <div class="content vertical">
            <div class="row two" v-if="item.descParamType==1">
              <div class="item" v-for="(subItem,index) in item.descr" :key="index">
                <label>{{subItem}}</label>
                <el-form-item
                  label="大於"
                  :prop="`list.${rowIndex}.${fieldArr[index]}`"
                  :rules="rules.numberRule"
                  v-if="index==0"
                >
                  <el-input v-model="item[fieldArr[index]]" size="small"></el-input>
                </el-form-item>
              </div>
            </div>
            <div class="row two" v-if="item.descParamType==2">
              <div class="item" v-for="(subItem,index) in item.descr" :key="index">
                <label>{{subItem}}</label>
                <el-form-item
                  label="大於"
                  :prop="`list.${rowIndex}.${fieldArr[2*index+index]}`"
                  :rules="rules.numberRule"
                >
                  <el-input v-model="item[fieldArr[2*index+index]]" size="small"></el-input>
                </el-form-item>
                <el-form-item
                  label="或小於"
                  :prop="`list.${rowIndex}.${fieldArr[2*index+index+1]}`"
                  :rules="rules.numberRule"
                >
                  <el-input v-model="item[fieldArr[2*index+index+1]]" size="small"></el-input>
                </el-form-item>
              </div>
            </div>
            <div class="row two" v-if="item.descParamType==3">
              <div class="item">
                <el-form-item
                  :label="subItem"
                  :prop="`list.${rowIndex}.${fieldArr[index]}`"
                  :rules="rules.numberRule"
                  v-for="(subItem,index) in item.descr"
                  :key="index"
                >
                  <el-input v-model="item[fieldArr[index]]" size="small"></el-input>
                </el-form-item>
              </div>
            </div>
            <template v-if="item.descParamType==4">
              <div class="row one" v-for="(subItem,index) in item.descr" :key="index">
                <div class="item">{{subItem}}</div>
                <div class="item">
                  <el-form-item
                    :label="index==0?'小於':'大於'"
                    :prop="`list.${rowIndex}.${fieldArr[index]}`"
                    :rules="rules.numberRule"
                  >
                    <el-input v-model="item[fieldArr[index]]" size="small"></el-input>
                  </el-form-item>
                </div>
              </div>
            </template>
            <!-- <div class="row multi-row" v-if="item.descParamType==4">
              multi-item       
            </div>-->
            <div class="row one">
              <el-form-item
                label="建議信息"
                :prop="`list.${rowIndex}.suggestion`"
                :rules="rules.suggestion"
              >
                <el-input
                  v-model="item.suggestion"
                  class="max-width"
                  size="small"
                  placeholder="請儘快處理"
                ></el-input>
              </el-form-item>
            </div>
          </div>
        </el-collapse-item>
      </el-collapse>
    </el-form>
  </div>
</template>

<script>
import setMixin from "./set-mixin";
import { alarmService } from "@/services/cold-station-service";
export default {
  mixins: [setMixin],
  watch: {
    alarmTmplData: {
      handler(val) {
        console.log("showAlarmSetWin end:>> ", val);
        if (val) {
          this.initData(2);
        }

         else{            this.$refs[“ruleForm”].resetFields();         }

      },
      deep:true,
      immediate: true
    }
  },
  methods: {
    onSubmit() {
      console.log("末端確定 :>> ");
      this.$refs["ruleForm"].validate(valid => {
        if (valid) {
          console.log("驗證成功");
          this.$emit("onSubmit", this.ruleForm.list, true);
        }
      });
    }
  }
};
</script>

<style lang="scss" scoped>
@import "./set.scss";
</style>

由於要兩個tab中都驗證通過時，才提交表單，所以兩個表單都要驗證，只有都驗證通過時在提交表單，提交表單之前，要合併表單數據再統一提交。父組件調用子組件的方法 this.$refs[“coldSet”].onSubmit();

考慮到彈窗組件的性能問題，我們可以通過將显示標識以 :showAlarmSetWin.sync=”showAlarmSetWin”這樣的形式傳遞給子組件，（注意，要加sync關鍵字）子組件監聽showAlarmSetWin，當彈窗显示時，加載數據並初始化，並設置屬性：immediate: true，讓彈窗第一次執行時也加載數據。

當窗體隱藏時，重置表單：
this.$refs[“ruleForm”].resetFields();
為了防止同一時間多次點擊操作按鈕“確定”，可以給按鈕加上loading
數據列表格式：

{
    "data": [{
        "id": 246,
        "tempId": "1",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 247,
        "tempId": "2",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 248,
        "tempId": "3",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 249,
        "tempId": "4",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 250,
        "tempId": "5",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 251,
        "tempId": "6",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 252,
        "tempId": "7",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 253,
        "tempId": "8",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 254,
        "tempId": "9",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 255,
        "tempId": "10",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 256,
        "tempId": "11",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 257,
        "tempId": "12",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 258,
        "tempId": "13",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 259,
        "tempId": "14",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 260,
        "tempId": "15",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 261,
        "tempId": "16",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 262,
        "tempId": "50",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 263,
        "tempId": "51",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 264,
        "tempId": "52",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 265,
        "tempId": "53",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 266,
        "tempId": "54",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 267,
        "tempId": "55",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 268,
        "tempId": "56",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 269,
        "tempId": "57",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 270,
        "tempId": "58",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 271,
        "tempId": "59",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 272,
        "tempId": "60",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 273,
        "tempId": "61",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 274,
        "tempId": "62",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 275,
        "tempId": "63",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 276,
        "tempId": "64",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 277,
        "tempId": "65",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 278,
        "tempId": "66",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 279,
        "tempId": "67",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 280,
        "tempId": "68",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 281,
        "tempId": "69",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 282,
        "tempId": "101",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 283,
        "tempId": "102",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 84.0,
        "secondVal": 16.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 284,
        "tempId": "103",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 59.0,
        "secondVal": 49.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 285,
        "tempId": "104",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 34.0,
        "secondVal": 22.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 286,
        "tempId": "105",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 92.0,
        "secondVal": 66.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 287,
        "tempId": "106",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 55.0,
        "secondVal": 29.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 288,
        "tempId": "107",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 86.0,
        "secondVal": 81.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 289,
        "tempId": "108",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 67.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 290,
        "tempId": "109",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 85.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 291,
        "tempId": "110",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 16.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 292,
        "tempId": "111",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 92.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 293,
        "tempId": "112",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": "請儘快安排人檢查",
        "firstVal": 10.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 294,
        "tempId": "113",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 44.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 295,
        "tempId": "114",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": "請儘快安排人檢查",
        "firstVal": 61.0,
        "secondVal": 35.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 296,
        "tempId": "115",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 48.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 297,
        "tempId": "116",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 298,
        "tempId": "117",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 299,
        "tempId": "118",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 76.0,
        "secondVal": 23.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 300,
        "tempId": "119",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 64.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 301,
        "tempId": "120",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 302,
        "tempId": "121",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 73.0,
        "secondVal": 15.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 303,
        "tempId": "122",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 90.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 304,
        "tempId": "201",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 305,
        "tempId": "202",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 306,
        "tempId": "203",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 307,
        "tempId": "204",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 32.0,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 308,
        "tempId": "205",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 309,
        "tempId": "206",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 310,
        "tempId": "207",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 311,
        "tempId": "208",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 312,
        "tempId": "209",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 313,
        "tempId": "210",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 314,
        "tempId": "211",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 315,
        "tempId": "212",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 316,
        "tempId": "213",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 317,
        "tempId": "214",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 318,
        "tempId": "215",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 319,
        "tempId": "216",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 320,
        "tempId": "217",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 321,
        "tempId": "218",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 322,
        "tempId": "219",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 323,
        "tempId": "220",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 36.0,
        "secondVal": 11.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 324,
        "tempId": "221",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": 66.0,
        "secondVal": 59.0,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }, {
        "id": 325,
        "tempId": "222",
        "projectNumber": "440300A088",
        "groupNumber": "G1",
        "alarmLevel": 1,
        "suggestion": null,
        "firstVal": null,
        "secondVal": null,
        "thirdVal": null,
        "fourthVal": null,
        "status": 0
    }],
    "code": 200,
    "msg": "成功",
    "errors": null
}

View Code

模板數據列表格式：

{
    "data": [{
        "id": "1",
        "name": "制冷機啟動失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"制冷機組設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "10",
        "name": "冷凍泵故障",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷凍水泵設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "101",
        "name": "冷凍水供水溫度不在合理範圍",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷凍水供水溫度\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "102",
        "name": "冷卻塔出水溫度溫度不在合理範圍",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷卻水回水溫度-室外濕球溫度(℃)\",\"或當室外濕球溫度<17℃時，冷卻水回水溫度設定值(℃)\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "103",
        "name": "冷凍供回水溫差（壓差）不在合理範圍",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷凍水溫差(℃)\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "104",
        "name": "冷卻供回水溫差不在合理範圍",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷卻水溫差(℃)\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "105",
        "name": "電流負載限制",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷水機組電流負載率\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "106",
        "name": "冷凝溫度限制",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷凝器出水溫度(℃)\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "107",
        "name": "蒸發溫度限制",
        "sys": 1,
        "type": 3,
        "descr": "[\"蒸發器出水溫度(℃)\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "108",
        "name": "蒸發器內水壓力超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"蒸發器冷媒壓力(Mpa)\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "109",
        "name": "蒸發器內水流量超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷凍水流量/當前制冷機的額定流量*製冷劑運行台數\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "11",
        "name": "冷卻泵啟動失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷卻水泵設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "110",
        "name": "冷凝器內水壓力超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷機冷凝器冷媒壓力(Mpa)\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "111",
        "name": "冷凝器內水流量超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷卻水流量/當前制冷機的額定流量*制冷機運行台數\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "112",
        "name": "冷凍水側小溫差過高",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，蒸發器出水溫度-冷媒溫度(℃)\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "113",
        "name": "冷卻水側小溫差過高",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷凝器冷媒溫度-出水溫度(℃)\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "114",
        "name": "冷凍水流量超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷凍泵流量/額定流量\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "115",
        "name": "冷凍泵功率超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷凍泵功率/額定功率\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "116",
        "name": "冷凍泵頻率超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷凍泵運行頻率不在配置的上下限範圍內\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "117",
        "name": "冷凍水溫差超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷凍水溫差在(3，7)範圍內\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "118",
        "name": "冷卻泵流量超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"冷卻泵流量/額定流量\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "119",
        "name": "冷卻泵功率超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷卻泵功率/額定功率\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "12",
        "name": "冷卻泵停止失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷卻水泵設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "120",
        "name": "冷卻塔頻率超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷卻塔頻率不在配置的上下限範圍\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "121",
        "name": "冷卻回水溫度超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷卻回水溫度\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "122",
        "name": "冷卻塔功率超限",
        "sys": 1,
        "type": 3,
        "descr": "[\"正常運行時段，冷卻塔功率/額定功率\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "13",
        "name": "冷卻泵故障",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷卻水泵設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "14",
        "name": "冷卻塔啟動失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷卻塔風機故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "15",
        "name": "冷卻塔停止失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷卻塔風機故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "16",
        "name": "冷卻塔故障",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷卻塔風機故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "2",
        "name": "制冷機停止失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"制冷機組設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "201",
        "name": "室內溫度傳感器需要校核",
        "sys": 2,
        "type": 4,
        "descr": "[\"每日6點，當前末端溫度反饋值與其他末端溫度反饋值相差2℃以上\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "202",
        "name": "工作時間前過早開啟空調末端",
        "sys": 2,
        "type": 2,
        "descr": "[\"工作時間前過早開啟空調末端\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "203",
        "name": "室外溫度高而新風閥未關閉",
        "sys": 2,
        "type": 2,
        "descr": "[\"室外溫度高而新風閥未關閉\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "204",
        "name": "室外溫度低而新風閥未開啟",
        "sys": 2,
        "type": 2,
        "descr": "[\"非營業時間，風櫃設定溫度-室外濕球溫度(℃)\",\"新風閥未開啟\"]",
        "descParamType": 1,
        "hasSuge": 1,
        "runTime": 3
    }, {
        "id": "205",
        "name": "空調風機變頻器自動控制未啟用",
        "sys": 2,
        "type": 2,
        "descr": "[\"當前時間<關機時間，室外濕球溫度>24且風櫃溫度人工設定\",\"或室外濕球溫度在[5,24]且風櫃溫度人工設定\",\"或室外濕球溫度<5且風櫃（風盤）溫度人工設定\"]",
        "descParamType": 4,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "206",
        "name": "室內CO2過高",
        "sys": 2,
        "type": 3,
        "descr": "[\"室內CO2(PPM)\",\"持續時間(min)\"]",
        "descParamType": 3,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "207",
        "name": "空調末端風機故障",
        "sys": 2,
        "type": 1,
        "descr": "[\"空調末端風機故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "208",
        "name": "空調末端新風閥故障",
        "sys": 2,
        "type": 1,
        "descr": "[\"空調末端新風閥故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "209",
        "name": "空調末端迴風閥故障",
        "sys": 2,
        "type": 1,
        "descr": "[\"空調末端迴風閥故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "210",
        "name": "空調末端水閥故障",
        "sys": 2,
        "type": 1,
        "descr": "[\"空調末端水閥故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "211",
        "name": "風櫃開啟失敗",
        "sys": 2,
        "type": 1,
        "descr": "[\"風櫃開啟失敗\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "212",
        "name": "風櫃停止失敗",
        "sys": 2,
        "type": 1,
        "descr": "[\"風櫃停止失敗\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "213",
        "name": "風盤開啟失敗",
        "sys": 2,
        "type": 1,
        "descr": "[\"風盤開啟失敗\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "214",
        "name": "風盤停止失敗",
        "sys": 2,
        "type": 1,
        "descr": "[\"風盤停止失敗\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "215",
        "name": "時序配置異常",
        "sys": 2,
        "type": 2,
        "descr": "[\"時序配置異常\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "216",
        "name": "末端設備為手動模式",
        "sys": 2,
        "type": 2,
        "descr": "[\"末端設備為手動模式\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "217",
        "name": "風櫃故障報警",
        "sys": 2,
        "type": 1,
        "descr": "[\"風櫃故障報警\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "218",
        "name": "風盤故障報警",
        "sys": 2,
        "type": 1,
        "descr": "[\"風盤故障報警\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "219",
        "name": "風櫃頻率超限",
        "sys": 2,
        "type": 3,
        "descr": "[\"風櫃頻率超限\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "220",
        "name": "室內溫度不在合理範圍",
        "sys": 2,
        "type": 3,
        "descr": "[\"風櫃迴風溫度(℃)\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "221",
        "name": "末端水力不平衡",
        "sys": 2,
        "type": 2,
        "descr": "[\"營業時間內，風櫃迴風溫度(℃)\"]",
        "descParamType": 2,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "222",
        "name": "風櫃頻率超限",
        "sys": 2,
        "type": 3,
        "descr": "[\"風櫃頻率CAB_FRQ不在配置的上下限範圍\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 2
    }, {
        "id": "3",
        "name": "制冷機故障",
        "sys": 1,
        "type": 1,
        "descr": "[\"制冷機組設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "4",
        "name": "制冷機冷凍側閥門啟動失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"制冷機組設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "5",
        "name": "制冷機冷凍側閥門停止失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"制冷機組設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "50",
        "name": "水力不平衡",
        "sys": 1,
        "type": 2,
        "descr": "[\"觸發冰爽模式\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "51",
        "name": "非變頻自動運行",
        "sys": 1,
        "type": 2,
        "descr": "[\"設備工頻啟停或頻率手動設定\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "52",
        "name": "全自動或一鍵啟動失敗",
        "sys": 1,
        "type": 2,
        "descr": "[\"全自動模式、一鍵啟動模式無法生效\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "53",
        "name": "過早開製冷站設備",
        "sys": 1,
        "type": 2,
        "descr": "[\"營業時間前過早開製冷站設備\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "54",
        "name": "停業后未及時停止製冷站設備",
        "sys": 1,
        "type": 2,
        "descr": "[\"停業后未及時停止製冷站設備\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "55",
        "name": "低溫未啟用全新風策略",
        "sys": 1,
        "type": 2,
        "descr": "[\"天氣溫度低而製冷站運行\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "56",
        "name": "制冷機加減載不合理",
        "sys": 1,
        "type": 2,
        "descr": "[\"手動模式下，執行制冷機的加減載\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "57",
        "name": "制冷機加減載失敗",
        "sys": 1,
        "type": 2,
        "descr": "[\"制冷機加減載失敗\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "58",
        "name": "冷水機組冷凍水旁通",
        "sys": 1,
        "type": 2,
        "descr": "[\"正常運行時段，運行狀態-停止狀態的冷機蒸發器進水溫度<1\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "59",
        "name": "冷水機組冷卻水旁通",
        "sys": 1,
        "type": 2,
        "descr": "[\"正常運行時段，運行狀態-停止狀態的冷機冷凝器進水溫度<1\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "6",
        "name": "制冷機冷卻側閥門啟動失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"制冷機組設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "60",
        "name": "制冷機頻繁啟停機",
        "sys": 1,
        "type": 2,
        "descr": "[\"設備啟停記錄中，同一設備的啟動和停止時間間隔<30min\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "61",
        "name": "冷卻泵頻繁啟停機",
        "sys": 1,
        "type": 2,
        "descr": "[\"設備啟停記錄中，同一設備的啟動和停止時間間隔<30min\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "62",
        "name": "冷凍泵頻繁啟停機",
        "sys": 1,
        "type": 2,
        "descr": "[\"設備啟停記錄中，同一設備的啟動和停止時間間隔<30min\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "63",
        "name": "冷卻塔頻繁啟停機",
        "sys": 1,
        "type": 2,
        "descr": "[\"設備啟停記錄中，同一設備的啟動和停止時間間隔<30min\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "64",
        "name": "未啟用控制模式",
        "sys": 1,
        "type": 2,
        "descr": "[\"冷凍泵運行頻率為手動設定或工頻運行\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "65",
        "name": "冷卻塔集水盤溢流",
        "sys": 1,
        "type": 2,
        "descr": "[\"冷卻塔液位COT1_WL>後台配置中的液位上限\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "66",
        "name": "冷卻塔集水盤乾涸",
        "sys": 1,
        "type": 2,
        "descr": "[\"冷卻塔液位COT1_WL<後台配置中的液位下限\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "67",
        "name": "冷卻塔啟停機不及時",
        "sys": 1,
        "type": 2,
        "descr": "[\"冷卻塔在主機停機后5min以外關閉\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "68",
        "name": "冷卻塔未啟用控制模式",
        "sys": 1,
        "type": 2,
        "descr": "[\"冷卻塔運行頻率為手動設定或工頻運行\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "69",
        "name": "冷卻泵啟停機不及時",
        "sys": 1,
        "type": 2,
        "descr": "[\"冷卻泵在主機啟動前2min以外啟動，或冷卻泵在主機停機后5min以外關閉\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 1
    }, {
        "id": "7",
        "name": "制冷機冷卻側閥門停止失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"制冷機組設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "8",
        "name": "冷凍泵啟動失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷凍水泵設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }, {
        "id": "9",
        "name": "冷凍泵停止失敗",
        "sys": 1,
        "type": 1,
        "descr": "[\"冷凍水泵設備故障\"]",
        "descParamType": 0,
        "hasSuge": 1,
        "runTime": 0
    }],
    "code": 200,
    "msg": "成功",
    "errors": null
}

View Code

總共兩個接口，一個加載模板，一個加載數據，模板數據只第一次進入到頁面的時候調用，數據是每次打開彈窗都要調用。

本站聲明:網站內容來源於博客園,如有侵權,請聯繫我們,我們將及時處理

※南投搬家公司費用需注意的眉眉角角，別等搬了再說!

上新台中搬家公司提供您一套專業有效率且人性化的辦公室搬遷、公司行號搬家及工廠遷廠的搬家服務

※台中搬家遵守搬運三大原則,讓您的家具不再被破壞!

台中搬家公司推薦超過30年經驗,首選台中大展搬家

等掌握了基礎知識之後，才有資格說基礎知識沒用這樣的話。否則就老老實實的開始吧。

 

 

對象的監視器

每一個Java對象都有一個監視器。並且規定，每個對象的監視器每次只能被一個線程擁有，只有擁有它的線程把它釋放之後，這個監視器才會被其它線程擁有。

其實就是說，對象的監視器對於多線程來說是互斥的，即一個線程從拿到它之後到釋放它之前這段時間內，其它線程是絕對不可能再拿到它的。這是由JVM保證的。

這樣一來，對象的監視器就可以用來保護那種每次只允許一個線程執行的方法或代碼片段，就是我們常說的同步方法或同步代碼塊。

Java包括兩種範疇的對象（當然，這樣講可能不準確，主要用於幫助理解），一種就是普通的對象，比如new Object()。一種就是描述類型信息的對象，即Class<?>類型的對象。

這兩類都是Java對象，這毋庸置疑，所以它們都有監視器。但這兩類對象又有明顯的不同，所以它們的監視器對外表現的行為也是不同的。

請看下面表達式：

 

Object o1 = new Object();Object o2 = new Object();o1 == o2; //false

 

o1和o2是分別new出來的兩個對象，它們肯定不相同。又因為監視器是和對象關聯的，所以o1的監視器和o2的監視器也是不同的，且它們沒有任何關係。

所以必須是同一個對象的監視器才行，不同對象的監視器達不到預期的效果，這一點要切記。

再看下面的表達式：

 

o1.getClass() == o2.getClass(); //trueo1.getClass() == Object.class; //true

 

但是o1的類型信息對象（o1.getClass()）和o2的類型信息對象（o2.getClass()）是同一個，且和Object類的類型信息對象（Object.class）也是同一個。這不廢話嘛，o1和o2都是從Object類new出來的。哈哈。

類型信息對象本身的類型是Class<?>，在類加載器（ClassLoader）加載一個類后，就會生成一個和該類相關的Class<?>類型的對象，該對象會被緩存起來，所以類型信息對象是全局（同一個JVM同一個類加載器）唯一的。

這也就說明了，為什麼同一個類new出來的多個對象是不同的，但是它們的類型信息對象卻是同一個，且可以使用“類.class”直接獲取到它。

Java語言規定，使用synchronized關鍵字可以獲取對象的監視器。下面分別來看這兩類對象的監視器用法。

普遍對象的監視器：

 

class SyncA { //方法A public synchronized void methodA() { //同步方法，當前對象的監視器 } //方法B public void methodB() { synchronized(this) { //同步代碼塊，當前對象的監視器 } }}
class SyncB { //對象 private SyncA syncA; public SyncB(SyncA syncA) { this.syncA = syncA; } //方法C public void methodC() { synchronized(syncA) { //同步代碼塊，syncA對象的監視器 } }}

//new一個對象SyncA syncA = new SyncA();//把該對象傳進去SyncB syncB = new SyncB(syncA);//A、B、C這三個方法都要擁有syncA這個對象的監視器才能執行new Thread(syncA::methodA).start();new Thread(syncA::methodB).start();new Thread(syncB::methodC).start();

 

這三個線程都去獲取同一個對象（即syncA）的監視器，因為一個對象的監視器一次只能被一個線程擁有，所以這三個線程是逐次獲取到的，因此這三個方法也是逐次執行的。

這個示例告訴我們，利用對象的監視器可以做到的，並不只是同一個方法不能同時被多個線程執行，多個不同的方法也可以不能同時被多個線程執行，只要它們用到的是同一個對象的監視器。

類型信息對象的監視器：

 

class SyncC { //靜態方法A public static synchronized void methodA() { //同步方法，類型信息對象的監視器 } //靜態方法B public static void methodB() { synchronized(SyncC.class) { //同步代碼塊，類型信息對象的監視器 } }}
class SyncD { //類型信息對象 private Class<SyncC> syncClass; public SyncD(Class<SyncC> syncClass) { this.syncClass = syncClass; } //方法C public void methodC() { synchronized(syncClass) { //同步代碼塊，SyncC類的類型信息對象的監視器 } } //方法D public void methodD() { synchronized(syncClass) { //同步代碼塊，SyncC類的類型信息對象的監視器 } }}

//A、B、C、D這四個方法都要擁有SyncC類的類型信息對象的監視器才能執行new Thread(SyncC::methodA).start();new Thread(SyncC::methodB).start();new Thread(new SyncD(SyncC.class)::methodC).start();new Thread(new SyncD((Class<SyncC>)new SyncC().getClass())::methodD).start();

 

因為一個類的類型信息對象只有一個，所以這四個線程其實是在競爭同一個對象的監視器，因此這四個方法也是逐次執行的。

通過這個示例，再次強調一下，不管是方法還是代碼塊，不管是靜態的還是實例的，也不管是屬於同一個類的還是多個類的，只要它們共用同一個對象的監視器，那麼這些方法或代碼塊在多線程下是無法併發運行的，只能逐個運行，因為同一個對象的監視器每次只能被一個線程所擁有，其它線程此時只能被阻塞着。

注：在實際使用中，一定要確保是同一個對象，尤其是使用字符串類型或数字類型的對象時，一定要注意。

幾個重要的方法

首先是Object類的wait/notify/notifyAll方法，因為Java中的所有類最終都繼承自Object類，所以，可以使用任何Java對象來調用這三個方法。

不過Java規定，要在某個對象上調用這三個方法，必須先獲取那個對象的監視器才行。再次提醒，監視器是和對象關聯的，不同的對象監視器也是不同的。

請看下面的用法：

 

//new一個對象Object obj = new Object();//獲取對象的監視器synchronized(obj) { //在對象上調用wait方法 obj.wait();}

 

很多人首次接觸這一部分的時候一般都會比較懵，主要是因為搞不清人物關係。

這裏的wait方法雖然是在對象（即obj）上調用的，但卻不是讓這個對象等待的。而是讓執行這行代碼（即obj.wati()）的線程（即Thread）在這個對象（即obj）上等待的。

這裏的線程是等待的“主體”，對象是等待的“位置”。比如學校開運動會時，會在操場上為每班劃定一個位置，並插上一個牌子，寫上班級名稱。

這個牌子就相當於對象obj，它表示一個位置信息。當學生看到本班牌子之後，就會自動去牌子後面排隊等待。

學生就相當於線程，當學生看到牌子就相當於當線程執行到obj.wait()，學生去牌子後面排隊等待就相當於線程在對象obj上等待。

當線程執行完obj.wait()后，就會釋放掉對象obj的監視器，轉而進入對象obj的等待集合中進行等待，線程由運行狀態變為等待（WAITING）狀態。此後這個線程將不再被線程調度器調度。

（說明一點，當多個線程去競爭同一個對象的監視器而沒有競爭上時，線程會變為阻塞（BLOCKED）狀態，而非等待狀態。）

線程選擇等待的原因大多都是因為需要的資源暫時得不到，那什麼時候資源能就位讓線程再次執行呢？其實是不太好確定的，那乾脆就到資源OK時通知它一聲吧。

請看下面的方法：

 

//獲取對象（還是上面那個）的監視器synchronized(obj) { //在對象上調用notify方法 obj.notify();}

 

有了上面的基礎，現在就好理解多了。代碼的意思就是通知在對象obj上等待的線程，把其中一個喚醒。即把這個線程從對象obj的等待集合中移除。此後這個線程就又可以被線程調度器調度了。可能有一部分人覺得現在被喚醒的那個線程就可以執行了，其實不然。

當前線程執行完notify方法后，必須要釋放掉對象obj的監視器，這樣被喚醒的那個線程才能重新獲取對象obj的監視器，這樣才可以繼續執行。

就是當一個線程想要通過wait進入等待時，需要獲取對象的監視器。當別的線程通過notify喚醒這個線程時，這個線程想要繼續執行，還需要獲取對象的監視器。

notifyAll方法的用法和notify是一樣的，只是含義不同，表示通知對象obj上所有等待的線程，把它們全部都喚醒。雖然是全部喚醒，但也只能有一個線程可以運行，因為每次只有一個線程能獲取到對象obj的監視器。

還有一種wait方法是帶有超時時間的，它表示線程進入等待的時間達到超時時間后還沒有被喚醒時，它會自動醒來（也可以認為是被系統喚醒的）。

這種情況下沒有超時異常拋出，雖然線程是自動醒來，但想要繼續執行的話，同樣需要先獲取對象obj的監視器才行。

注：線程通過wait進入等待時，只會釋放和這個wait相關的那個對象的監視器。如果此時線程還擁有其它對象的監視器，並不會去釋放它們，而是在等待期間一直擁有。這塊一定要注意，避免死鎖。

使用須知：

處在等待狀態的線程，可能會被意外喚醒，即此時條件並不滿足，但是卻被喚醒了。當然，這種情況在實踐中很少發生。但是我們還是要做一些措施來應對，那就是再次檢測條件是否滿足，不滿足的話再次進入等待。

可見這是一個具有重複性的邏輯，因此把它放到一個循環里是最合適的，如下這樣：

 

//獲取對象的監視器synchronized(obj) { //判斷條件是否滿足 while(condition is not satisfied) { //在對象上調用wait方法 obj.wait(); }}

 

這樣一來，即使被意外喚醒，還會再次進入等待。直到條件滿足后，才會退出while循環，執行後面的邏輯。

多線程的話題怎麼能少了主角呢，下面有請主角上場，哈哈，就是Thread類啦。關於線程，我在上一篇文章中已經談過，這裏再贅述一遍，希望加深一下印象。

線程是可以獨立運行的“個體”，這就導致我們對它的“控制能力”變弱了。當我們想讓一個線程暫停或停止時，如果強制去執行，會產生兩方面的問題，一是使正在執行的業務中斷，導致業務出現不一致性。二是使正在使用的資源得不到釋放，導致內存泄漏或死鎖。可見，強制這種方式不可取。（看看Thread類的那些廢棄方法便知）

所以，只能採取柔和的方式，就是你對一個線程說，“大哥，停下來歇會吧”，或者是，“大哥，停止吧，不用再執行了”。雖然聽着是噁心了點，但意思就是這樣的。那麼當線程接收到這個“話語”時，它必須要做出反應，自己讓自己停止，當然，線程也可以根據自己的需要，選擇不停止而繼續執行。

這才是和線程交互最安全的方式，就像一個高速行駛的汽車，只有自己慢慢停下來才是最好的方式，直接通過外力干預，很大概率是車毀人亡。

這種柔和的處理方式，在計算機里有個專用名詞，叫中斷。這是一種交互方式，你對別人發送一个中斷，別人要響應這个中斷並做出相應的處理。如果別人不響應你的這个中斷，那隻能是“熱臉貼冷屁股”，完全沒了面子。可見，參与中斷的雙方必須要提前約定好，你怎麼發送，別人怎麼處理，否則只能是雞同鴨講。

Thread類和中斷相關的方法有三個：

實例方法，void interrupt()，表示中斷線程，要中斷哪個線程就在哪個線程的對象上調用該方法。

※台中搬家公司費用怎麼算?

擁有20年純熟搬遷經驗，提供免費估價且流程透明更是5星評價的搬家公司

 

Thread t = new Thread(() -> {doSomething();});t.start();t.interrupt();

 

new一個線程，啟動它，然後中斷它。

當一個線程被其它線程中斷後，這個線程必須要能檢測到自己被中斷了才行，於是就有了下面這個方法。

實例方法，boolean isInterrupted()，返回一個線程是否被中斷。常用於一個線程檢測自己是否被中斷。

 

if(Thread.currentThread().isInterrupted()) { doSomething(); return;}

 

如果線程發現自己被中斷，做一些事情，然後退出。該方法只會去讀取線程的中斷狀態，而不會去修改它，所以多次調用返回同樣的結果。

線程在處理中斷前，需要將中斷狀態清除一下，即將它設置成false。否則下次檢測時還是true，以為又中斷了呢，實則不是。

靜態方法，static boolean interrupted()，該方法有兩個作用，一是返回線程是否被中斷，二是如果中斷則清除中斷狀態。

 

Thread.interrupted();

 

由於這個方法是靜態方法，所以只能用於當前線程，即線程自己清除自己的中斷狀態。

由於這個方法會清除中斷狀態，所以，如果第一次調用返回true的話，緊接着再調用一次應該返回false，除非在兩次調用之間線程真的又被中斷了。

還有一種特殊情況就是，在你中斷一個線程時，這個線程恰巧沒有在運行，它可能是因為競爭對象的監視器“失敗”（即沒有爭取上）而處於阻塞狀態，可能是因為條件不滿足而處於等待狀態，可能是因為在睡眠中。總之，線程目前沒有在執行代碼。

由於線程目前沒有在執行代碼，所以根本就無法去檢測這个中斷狀態，也就是無法響應中斷了，這樣肯定是不行的。所以設計者們此時選擇了拋異常。

因此，不管是由於阻塞/等待/睡眠，只要一個線程處於“停止”（即沒有在運行）時，此時去中斷它，線程會被喚醒，接着同樣要去再次獲取監視器，然後就收到了InterruptedException異常了，我們可以捕獲這個異常並處理它，使線程可以繼續正常運行。此時既然已經收到異常了，所以中斷狀態也就同時給清除了，因為中斷異常已經足夠表示中斷了。

仔細想想這種設計其實頗具人性化。就好比一個人，在他醒着的時候，跟他說話，他一定會回應你。當他睡着時，跟他說話，其實他是聽不到的，自然無法回應你。此時應該採取稍微暴力一點的手段，比如把他搖晃醒。

所以，一個線程正在運行時，去中斷它，是不會拋異常的，只是設置中斷狀態。此時中斷狀態就表示了中斷。一個線程在沒有運行時（阻塞/等待/睡眠），去中斷它，會拋出中斷異常，同時清除中斷狀態。此時中斷異常就表示了中斷。

然後就是sleep方法，表示線程臨時停止執行一段時間，這裏只有一個要點，就是在睡眠期間，線程擁有的所有對象的監視器都不會被釋放。

 

Thread.sleep(1000);

 

由於sleep是靜態方法，所以，一個線程只能讓自己睡眠，而沒有辦法讓別的線程睡眠，這是完全正確的，符合我們一直在闡述的思想。一個線程的行為應該由自己掌控，別的線程頂多可以給你一个中斷而已，而且你還可以選擇處理它或忽略它。

最後一個方法是join，它是一個實例方法，所以需要在一個線程對象上調用它，如下：

 

Thread t = new Thread(() -> {doSomething();});t.start();t.join();

 

表示當前線程執行完t.join()代碼后，就會進入等待，直到線程t死亡后，當前線程才會重新恢復執行。我在上一篇文章中把它比喻為插隊，線程t插到了當前線程的前面，所以必須等線程t執行完后，當前線程才會接着執行。

這裏主要是想說下它的源碼實現，join方法標有synchronized關鍵字，所以是同步方法，而且在方法體內調用了從Object類繼承來的wait方法。

所以join方法可以這樣來解釋，當前線程獲取到線程對象t的監視器，然後執行t.wait()，使當前線程在線程對象t上等待，當前線程從運行狀態進入到等待狀態。由於對象t是一個線程，這是非常特殊的，因為線程執行完是會終止的，且在終止時會自動調用notifyAll方法進行通知。

有句話是這樣講的，“鳥之將死，其鳴也哀；人之將死，其言也善”。因此，一個線程都快要死了，是不是應該通知在自己身上等待的其它所有線程，把大夥都喚醒。總不能讓所有人都給自己“陪葬”吧，哈哈。

因此，在線程t執行結束后，會自動執行t.notifyAll()來通知所有在t上等待的線程，並把它們全部喚醒。所以當前線程會繼續接着執行。

為什麼說notifyAll()是自動執行的呢？因為源碼中並沒有去調用它，而實際卻執行了，所以只能是系統自動調用了。

所以，從宏觀上看，就是當前線程在等待線程t的死亡。

任何Java對象都有監視器，所以線程對象也有監視器，但線程對象確實比較特殊，所以它的wait/notify方法也會有特殊的地方，因此官方建議我們不要隨意去玩Thread類的這些方法。

 

完整示例源碼：

https://github.com/coding-new-talking/java-code-demo.git

 

如果以上內容閣下全部都知道，而且理解到位，那已經很厲害了，請等待下篇多線的文章吧。

 

 

（END）

 

作者是工作超過10年的碼農，現在任架構師。喜歡研究技術，崇尚簡單快樂。追求以通俗易懂的語言解說技術，希望所有的讀者都能看懂並記住。下面是公眾號的二維碼，歡迎關注！

 

本站聲明:網站內容來源於博客園,如有侵權,請聯繫我們,我們將及時處理

※台中搬家公司費用怎麼算?

擁有20年純熟搬遷經驗，提供免費估價且流程透明更是5星評價的搬家公司

※回頭車貨運收費標準

宇安交通關係企業，自成立迄今，即秉持著「以誠待人」、「以實處事」的企業信念

1萬最值得表揚的地方：外觀絕對算是最滿意的，很漂亮時尚，大氣穩重，改款后增加的配置也很多，內飾也上檔次了，空間也能滿足家庭日常使用，給人很寬敞的感覺，動力完全夠用，性價比非常高。尚有不足：整車做工方面還有待提高，一擋換二擋有點不順暢，低扭有點不足，後排座椅不能比例放倒。

長安汽車-逸動

指導價：8.09-24.99萬

基本資料

長*寬*高(mm) 4620*1820*1490

軸距(mm) 2660

動力系統

1.6L+5擋手動/4擋手自一體

車主一

購買車型：2016款 1.6L 手動風尚型

裸車價格：7.1萬

最值得表揚的地方：外觀絕對算是最滿意的，很漂亮時尚，大氣穩重，改款后增加的配置也很多，內飾也上檔次了，空間也能滿足家庭日常使用，給人很寬敞的感覺，

※智慧手機時代的來臨，RWD網頁設計為架站首選

網動結合了許多網際網路業界的菁英共同研發簡單易操作的架站工具，及時性的更新，為客戶創造出更多的網路商機。

動力完全夠用，性價比非常高。

尚有不足：整車做工方面還有待提高，一擋換二擋有點不順暢，低扭有點不足，後排座椅不能比例放倒。

車主二

購買車型：2016款 1.6L 自動風尚型

裸車價格：7.5萬

最值得表揚的地方：外觀時尚動感，線條流暢，給人十分耐看而大氣的感覺，小改款后的內飾中控台材質有改良過，質感比較好，主被動安全配置明顯提高了，乘坐空間和舒適性都令人滿意，綜合實力強。

尚有不足：後排座椅沒有中間頭枕，油耗稍微高點，液壓助力方向盤有點重，4AT變速箱有點落後，開起來感覺比較肉。

編輯點評：逸動在自主品牌當中做工算是比較出色的，但細節上還和合資品牌有一定差距，配置上已經跟得上主流，但是發動機、變速箱等技術還有待進一步提升。本站聲明:網站內容來源於http://www.auto6s.com/,如有侵權,請聯繫我們,我們將及時處理

※評比南投搬家公司費用收費行情懶人包大公開

搬家價格與搬家費用透明合理，不亂收費。本公司提供下列三種搬家計費方案，由資深專業組長到府估價，替客戶量身規劃選擇最經濟節省的計費方式

※想知道購買電動車哪裡補助最多?台中電動車補助資訊懶人包彙整

節能減碳愛地球是景泰電動車的理念，是創立景泰電動車行的初衷，滿意態度更是服務客戶的最高品質，我們的成長來自於你的推薦。

除了最低配車型都配置了一鍵啟動和無鑰匙進入，而一鍵啟動按鈕則“別出心裁”地放在了儀錶台左側。高配車型有着6安全氣囊的配置，在同價位車型中處於優勢地位。接近緊湊型的軸距使得DX3有着一個在同級別中相當不錯的後排空間。

前言

對於東南汽車，不少人都知道它曾經是三菱在中國的合作夥伴，在相互合作之中積累不少三菱的技術以及經驗，所以在底盤研究上在國產品牌中是處於比較優秀的地位，而且也捨得成本在研發以及底盤設計用料上，而今天介紹的東南DX3就是這樣的一個例子。

東南DX3定位在緊湊型DX7之下，是一輛面向年輕人市場為主的小型SUV，車身尺寸為4354*1840*1670mm，與比亞迪元、長安CS15這些競爭對手相比都有着一定的優勢。

東南汽車一直是一個非常實在的車企，在造型設計一直都保持了自己的原創，而且外觀上也有着日系的風格，所以這輛DX3在外觀上能夠吸引不少年輕人的目光。前臉使用交錯的線條使得它非常年輕活動，而保險杠下的銀色下護板又有着一種下唇的感覺，比較有競技氣息。

在車身側面可以看到採用了懸浮式設計，車身腰線一直延續到尾燈之上，在後輪輪拱位置更是往外拋出使得它显示出力量感。

但是在車尾部就有着一種虎頭蛇尾的感覺，和車頭形成了強烈對比，不過也算的是比較協調耐看。

輪轂方面分別有着17英寸以及18英寸的雙色鋁合金輪轂可供選擇，

※南投搬家公司費用,距離,噸數怎麼算?達人教你簡易估價知識!

搬家費用：依消費者運送距離、搬運樓層、有無電梯、步行距離、特殊地形、超重物品等計價因素後，評估每車次單

輪胎規則為215/55R 18，規格較高，但是在品牌上選擇的是名氣較小的萬力輪胎。

內飾設計也是原創度極高，中控放着一個9英寸的多媒體显示屏，相當大氣。而純黑色的設計相當的運動，而且看上去也更具檔次。

採用了這種螺旋形空調出風口，非常時尚好看，但是想要在出風口插手機支架的用戶看來要換成磁吸的了。

簡單易讀的儀錶盤，在底色上使用了紅色作為主調，儀錶中心還有着一個小显示屏可以显示部分車輛信息。

全系標配了ESp車身穩定系統以及陡坡緩降系統，相當良心。

除了最低配車型都配置了一鍵啟動和無鑰匙進入，而一鍵啟動按鈕則“別出心裁”地放在了儀錶台左側。

高配車型有着6安全氣囊的配置，在同價位車型中處於優勢地位。

接近緊湊型的軸距使得DX3有着一個在同級別中相當不錯的後排空間。

另有還有着一個全景天窗可以帶來明亮的車廂環境，非常受年輕人喜愛。

動力有着一個最大功率為88千瓦的1.5L自然發動機以及最大功率為115千瓦的1.5T渦輪增壓發動機選擇，1.5L自然吸氣發動機版本全系搭配手動變速箱，而1.5T渦輪增壓發動機版本全系搭配CVT自動變速箱，總體處於主流水平。

底盤上使用的是前麥費遜后多連桿獨立懸架，相對於同價位中多半使用后非獨立懸架能帶來更優秀的駕駛體驗以及乘坐體驗。

總的來說這是一輛非常適合年輕人選擇的小型SUV，有着不低的顏值、夠用的空間，以及是同級別中優秀的安全配置以及駕駛性能，預售價為7.29-9.99萬，依然算的是親民。本站聲明:網站內容來源於http://www.auto6s.com/,如有侵權,請聯繫我們,我們將及時處理

※網頁設計公司推薦不同的風格，搶佔消費者視覺第一線

透過選單樣式的調整、圖片的縮放比例、文字的放大及段落的排版對應來給使用者最佳的瀏覽體驗，所以不用擔心有手機版網站兩個後台的問題，而視覺效果也是透過我們前端設計師優秀的空間比例設計，不會因為畫面變大變小而影響到整體視覺的美感。